Estructura según en pseint.

Estructura según en pseint.

a variable pueda un valor de entre varios. Por ejemplo, en el sistema de notas escolares español clásico, ciertas notas numéricas tienen "nombres" asociados: un 5 es un aprobado, un 9 y un 10 son sobresaliente, etc. Si queremos hacer un programa que convierta de la nota numérica a su equivalente escrito, podríamos emplear varias órdenes IF, una tras la otra. Pero en muchos lenguajes de programación (y por tanto, también en muchas variantes de pseudocódigo) existe una alternativa más compacta y más legible: la orden "SEGUN". Esta órden permite hacer unas cosas u otras según el valor que tome una variable. Su uso sería así:

Segun variable Hacer
  valor1: pasos_a_dar_si_es_el_valor1Es frecuente tener que comprobar más de una condición a la vez, o bien varias condiciones consecutivas. En concreto, un caso especialmente habitual es el de que un
  valor2: pasos_a_dar_si_es_el_valor2
  valor3: pasos_a_dar_si_es_el_valor3
De Otro Modo:
  pasos_a_dar_si_es_otro_valor
FinSegun

El bloque "De Otro Modo" es opcional: si detallamos todos los valores posibles, no sería necesario utilizarlo.

El número de valores que podemos probar es indefinido: no tiene por qué ser 3, sino que pueden ser menos casos o muchos más.

Según la variante de pseudocódigo (o el lenguaje de programación) que empleemos, puede haber restricciones en el tipo de datos que es aceptable. Por ejemplo, en el caso de PseInt, la variable tiene que tener un valor numérico, no puede ser un texto.

Al igual que ocurría con la orden SI, existe un símbolo que podemos usar en los diagramas de flujo para ayudarmos a planificar nuestro programa (aunque este símbolo está menos extendido que el de SI):

Así, si en PseInt hacemos clic en el icono del panel derecho que representa la condición SEGUN, aparece un esqueleto de programa casi completo, para que hagamos los cambios que nos interesen:

 http://www.aprendeaprogramar.com/mod/resource/view.php?id=403

Estructura si entonces en pseint.

Estructura si entonces en pseint.

Condicional Si-Entonces

La secuencia de instrucciones ejecutadas por la instrucción Si-Entonces-Sino depende del valor de una condición lógica.

Ejemplo 1

      

Al ejecutarse esta instrucción, se evalúa la condición y se ejecutan las instrucciones que correspondan: las instrucciones que le siguen al Entonces si la condición es verdadera, o las instrucciones que le siguen al Sino si la condición es falsa. La condición debe ser una expresión lógica, que al ser evaluada retorna Verdadero o Falso. 

La cláusula Entonces debe aparecer siempre, pero la cláusla Sino puede no estar. En ese caso, si la condición es falsa no se ejecuta ninguna instrucción y la ejecución del programa continúa con la instrucción siguiente.

 Ejemplo 2

Si <condición>

            Entonces

                 <instrucciones>

            Sino

                  <instrucciones>

      FinSi 

http://gerbermonterroso.blogspot.com/

Diagramas de flujo en pseint.

• Diagramas de flujo en pseint.

• 
• Presenta herramientas de edición para escribir algoritmos en pseudocodigo en españolAuto completadoAyudas EmergentesPlantillas de ComandosColoreado de SintaxisIndentado InteligentePermite generar y editar el diagrama de flujo del algoritmoPermite la edición simultánea de múltiple algoritmosEl lenguaje pseudocódigo utilizado es configurableOfrece perfiles de configuración predefinidos para numerosas institucionesPuede interpretar (ejecutar) los algoritmos escritosPermite ejecutar el algoritmo paso a paso controlando la velocidad e inspeccionando variables y expresionesPuede confeccionar automáticamente una tabla de prueba de escritorioDetermina y marca claramente errores de sintaxis (mientras escribe) y en tiempo de ejecuciónPermite convertir el algoritmo de pseudocódigo a código C++Ofrece un sistema de ayuda integrado acerca del pseudocódigo y el uso del programa
• 
• 
  
• https://aritlocovrblog.wordpress.com/2014/09/01/pseint-conceptos-y-caracteristicas/

Tipos de datos que usa pseint.

En el mundo de la programación se manejan mucha información, la cual esta conformada por datos. 
¿Qué son datos? 
Los datos son un conjunto de caracteres. 
¿Qué es un caracter? 
Un carácter puede ser una letra, un numero, un símbolo. 
Entonces teniendo en cuenta esos pequeños conceptos podremos decir que: Información es el conjunto organizado de datos cuyo propósito es informar acerca de un suceso determinado. 
Los lenguajes de programación han optado en clasificar esos datos para indicar al ordenador que clase de operación se va a procesar. 
La mayoría de los lenguajes de programación son lenguajes tipados, o sea tienen predefinidos un estándar en cuanto se refiere a los datos. 
Los tipos de datos mas comunes son enteros, reales(decimales), caracteres(cadenas de texto), y lógicos. 
En PseInt tenemos los siguientes tipos de datos: 

Tipo Real: Una variable de tipo real admite datos numéricos, que pueden ser enteros y/o con punto decimal.

Tipo Entero: Es una especialización que sólo permite almacenar valores enteros; cualquier valor no entero que se lea o asigne en una variable de este tipo será truncado.

Tipo Cadena: Es una secuencia ordenada (de longitud arbitraria, aunque finita) de elementos que pertenecen a un cierto lenguaje formal o alfabeto análogas a una fórmula o a una oración.

Tipo Carácter: Las variables de caracteres se usan para almacenar valores alfabéticos, en particular letras solas.

Tipo Lógico: Una variable de tipo LÓGICO sólo puede tomar los valores VERDADERO y FALSO, pero cuando se lee una variable ya definida como lógica, el usuario puede ingresar también las abreviaciones V y F, o 0 y 1.

https:///2016/09/20/tipos-de-datos-en-pseint/

¿Que es un pseucódigo?

¿Que es un pseucódigo?

La palabra pseudocódigo formada por el prefijo “pseudo“, que según el diccionario de la RAE (Real Academia Española) significa “falso“, de ahí parte para que también sea conocido como “falso lenguaje”.

Dentro de la programación se basa en un lenguaje de programación real, donde se permite expresar las instrucciones en un lenguaje común (ejemplo: español, inglés u otro idioma) para facilitar la escritura y lectura, debido a que está en lenguaje común si requiere una modificación es fácil hacerla. La escritura sólo puede ser comprendida por el ser humano y no por la máquina, por ende, tampoco puede ejecutarla. La finalidad de un pseudocódigo es representar la solución a un algoritmo (problema) de la forma más detallada posible, utilizando acciones sucesivas. Según Analía Lanzillotta: “Considerado como un lenguaje falso el pseudocódigo, que es un lenguaje intermedio entre nuestro lenguaje y el de programación, debido a que quien lo utiliza se guía por una serie de normas, pero sin llegar a usar una estructura tan rígida como la del lenguaje de programación”.Liga

En otras palabras, el pseudocódigo es un lenguaje simplificado entre el programador y la máquina, hecho por el programador en su propio idioma, para describir un algoritmo y  poder comprender mejor la estructura de dicho programa, donde el lenguaje simplificado no puede ser compilado, ejecutado ni corrido por la máquina. Siendo una herramienta que se encuentra previa al lenguaje formal de programación.

Ejemplo de la aplicación del pseudocódigo

Por ejemplo, un programador tiene que hacer un programa con un fin determinado, utiliza un pseudocódigo propio. En donde influye su lenguaje y algunas palabras de programación (inicio y fin e instrucciones específicas), después ocurre la traducción al lenguaje de programación (donde ya puede ser comprendido por la máquina).

En pseudocódigo

1 2 3 4 5

bilbliotecas inicio      Mostrar el mensaje de "hola, estás usando C++" fin

https://michelletorres.mx/que-es-el-pseudocodigo/

¿Qué es PSeInt?

¿Qué es PSeInt?

• PSeInt es una herramienta para asistir a un estudiante en sus primeros pasos en programación. Mediante un simple e intuitivo pseudolenguaje en español (complementado con un editor de diagramas de flujo), le permite centrar su atención en los conceptos fundamentales de la algoritmia computacional, minimizando las dificultades propias de un lenguaje y proporcionando un entorno de trabajo con numerosas ayudas y recursos didácticos.
• 

http://pseint.sourceforge.net/

"TIPOS DE ALGORITMOS"

Significado de algoritmo

¿Qué es un algoritmo? Se denomina algoritmo a una combinación de pasos lógicos dispuestos de forma organizada para resolver un problema. Los algoritmos ayudan a ordenar el trabajo en numerosas disciplinas. En informática se utilizan para expresar las ‘instrucciones’ con las que se realizan las funciones, y se suele expresar mediante diferentes tipos de diagrama. El esquema más conocido es el diagrama de flujo, que muestra paso por paso como se debe proseguir, y principalmente, las preguntas que el operador se debe hacer para proseguir con el siguiente paso y así llegar al final del proceso. Si algún paso falla, el algoritmo permite “retroceder ordenadamente” la cantidad de pasos que sean necesarios para corregir el error.

Clasificación y Tipos de algoritmos

Se ha clasificado a los algoritmos de diversas formas, de acuerdo con algunos de sus atributos. Por ejemplo:

A) Según el sistema de signos con el que describen los pasos a seguir, se reconocen:
–Algoritmos cualitativos: cuando se hace a través de palabras, es decir, las instrucciones son verbales. Sucede, por ejemplo, con recetas de cocina.
–Algoritmos cuantitativos: cuando se hace a través de cálculos numéricos. Se puede hacer un algoritmo, por ejemplo, para obtener la raíz cuadrada de un número.

B) Según su función, los algoritmos pueden ser:
–Algoritmos de ordenamiento: secuencian los elementos que ingresan a partir de un cierto orden, en general, según un orden numérico o léxico.
–Algoritmos de búsqueda: al contrario de realizar operaciones o secuenciar elementos, se dedica a encontrar dentro de una lista que ingresa, uno o varios elementos en particular que cumplan con el conjunto de condiciones dadas.
–Algoritmos de encaminamiento: deciden de qué modo se deberá transmitir algo que llega, y cómo seguirá un conjunto de pasos encadenados. Se dividen fundamentalmente entre adaptativos y estáticos, los primeros con cierta capacidad de aprendizaje y ajuste a la circunstancia, mientras que los segundos funcionan mecánicamente, siempre del mismo modo. Es importante decir que los algoritmos de encaminamiento cuentan con una propia subdivisión, según el camino que se toma para que la transmisión llegue de manera efectiva (ejemplos de estos tipos son: por el camino más corto, de manera óptima, basado en el flujo, etc.).

C) También los algoritmos han sido clasificados según la estrategia que se utiliza para llegar al resultado. Veamos algunos ejemplos:
–Algoritmos probabilísticos: no se puede estar seguro de la exactitud de la respuesta que darán. Se agrupan en distintos subtipos, pero con esa premisa: o bien presentan soluciones aproximadas del problema, o bien presentan soluciones que pueden ser correctas pero también erróneas.
–Algoritmo cotidiano: es el que se da en la vida común de las personas, no se aplica en sistemas informáticos ni en nada ajeno al día a día. Muchas de las decisiones que se toman desde que uno se despierta por la mañana pertenecen a este grupo.
–Algoritmo heurístico: abandona alguno de los objetivos como recurso para terminar llegando a la solución. En general, son utilizados cuando no existe una solución mediante las vías tradicionales.
–Algoritmo de escalada: se comienza con una solución insatisfactoria (que no cumple la entrada y la salida), y se la va modificando aproximándose a lo que se busca. En algún momento, estaremos cerca de (o llegaremos a) la solución correcta.
–Algoritmo voraz: Con la idea de llegar a una solución óptima definitiva, elige analizar cada paso como único y elegir la solución óptima para ese paso.
–Algoritmo determinista: es completamente lineal (cada paso tiene un paso sucesor y un paso predecesor) y por lo tanto predictivo, si se conocen sus entradas y su forma de proceder. El algoritmo de Euclides, que permite averiguar el máximo común divisor entre dos números, responde a este tipo. Se distinguen de los no deterministas, donde el algoritmo tiene un comportamiento en forma de árbol. 
Fuente: https://www.tiposde.org/ciencias-exactas/843-tipos-de-algoritmos/#ixzz5QfDJKx4L

Fuente: https://www.tiposde.org/ciencias-exactas/843-tipos-de-algoritmos/#ixzz5QfDEitf8

UNA VEZ QUE HEMOS VISTO LA INTRODUCCIÓN Y LA CLASIFICACIÓN DE ALGORITMOS NOS ENFOCAREMOS EN CUALITATIVOS Y CUANTITATIVOS.


EJEMPLOS DE ALGORITMOS CUALITATIVOS

1. Ver una película en un cine

INICIO

1.- ir al cinear la boleta

3.-entrar al cine

4.-ver la película

5- salir del cine

FIN

ALGORITMOS CUANTITATIVOS

1. Un numero multiplicado por otro

INICIO a) Num1=0, Num2=0, Multiplicacion=0 b) Escribir "Ingrese el numero 1", Leer Num1 c) Escribir "Ingrese el numero 2", Leer Num2 d) Multiplicacion=Num1*Num2 e) Escribir "La Respuesta Es: ", Multiplicacion FIN 

2. Construcción del Algoritmo:

1. Inicio ## Inicia la ejecución del programa.
2. Suministrar cifra de altura
3. Leer “h”
4. Suministrar cifra de base 
5. Leer“b”
6. A ← b*h/2 ## Asignar a "A" el resultado de multiplicar las cifras de base y altura y luego dividir el resultado de la multiplicación entre 2.
7. Generar resultado
8. Imprimir "A"
9. Fin ## Inicia la ejecución del programa.

http://programacionime2017me.blogspot.com/2017/10/ejemplos-de-algoritmos-cualitativos-y.html

FUNDAMENTOS DE PROGRAMACIÒN

 ¿EN QUÉ CONSISTE LA SOLUCIÓN DE PROBLEMAS?

Definición de Resolución de problemas Resolución de problemas:

Es el proceso a través del cual podemos reconocer las señales que identifican la presencia de una dificultad, anomalía o entorpecimiento del desarrollo normal de una tarea, recolectar la información necesaria para resolver los problemas detectados y escoger e implementar las mejores alternativas de solución, ya sea de manera individual o grupal. Cada situación es una oportunidad para que las personas sean capaces de transformar y mejorar continuamente el entorno en forma activa y además aprender de ello. Aplicada al mundo laboral, la resolución de problemas permite mantener el correcto desarrollo de las actividades, tareas o procesos, y estar preparado para enfrentar de manera eficiente los entorpecimientos cotidianos que se presentan en la ejecución de una labor.

COMPETENCIAS DEL ÁREA:

1. Recolectar, organizar y analizar la información que resuelve el problema.

2. Aplicar alternativas de solución de problemas.

3. Resolver problemas interpersonales.

Ampliar las posibilidades de éxito en la resolución de un problema supone, primero, identificar y seleccionar la mejor alternativa de solución. Sabemos que existen diferentes miradas y posibilidades de solución para un mismo problema, pero no siempre actuamos en consecuencia. Por ejemplo, por encontrarnos en una situación de urgencia, aplicamos la alternativa que tenemos más a mano. O, tenemos un punto de vista diferente al de otra persona y queremos imponer el nuestro. Digamos que ampliar la gama de alternativas generalmente permitirá ampliar las posibilidades de éxito, en la resolución de problemas, y, agreguemos que toda idea propuesta será válida en la medida que atienda el problema y se oriente al cumplimiento de objetivos previamente fijados.

BIBLIOGRAFÌA: http://ww2.educarchile.cl/UserFiles/P0029/File/Objetos_Didacticos/TPEmpleabilidad/modulo6/Recursos_conceptuales_RESOLUCION_PROBLEMAS_%20APLICAR_ALTERNATIVAS_DE_SOLUCION.pdf

PLANTEAMIENTO DE SOLUCIÒN DE PROBLEMAS SEGÚN POLYA.

Método Pólya.

 Origen Miller (2006) comenta que el 13 de diciembre de 1887 en Hungría nació un científico matemático llamado George Pólya. Estudió en la Universidad de Budapest; donde abordó temas de probabilidad. Luego en 1940 llegó a la Universidad de Brown en E.U.A. y pasó a la Universidad de Stanford en 1942 como maestro. Elaboró tres libros y más de 256 documentos, donde indicaba que para entender algo se tiene que comprender el problema. George Pólya investigó muchos enfoques, propuestas y teorías; su teoría más importante fue la Combinatoria. El interés en el proceso del descubrimiento y los resultados matemáticos llegaron en él, despertar el interés en su obra más importe la resolución de problemas. Se enfatizaba en el proceso de descubrimiento más que desarrollar ejercicios sistematizados. Pólya después de tanto estudio matemático murió en 1985 a la edad de 97 años; enriqueció la matemática con un importante legado en la enseñanza en el área para resolver problemas, dejando diez mandamientos para los profesores de matemática: 8

 Interés en la materia. 

 Conocimiento de la materia.

 Observar las expectativas y dificultades de los estudiantes. 

 Descubrir e investigar. 

 Promover actitudes mentales y el hábito del trabajo metódico. 

 Permitir aprender a conjeturar. 

 Permitir aprender a comprobar. 

 Advertir que los rasgos del problema que tiene a la mano pueden ser útiles en la solución de problemas futuros. 

 No mostrar todo el secreto a la primera: dejar que los estudiantes hagan las conjeturas antes.

 Sugerir; no obligar que lo traguen a la fuerza. 

Esta característica de dar una especie de paso creativo en la solución, no importa que tan pequeño sea, es lo que distingue un problema de un ejercicio. Sin embargo, es prudente aclarar que esta distinción no es absoluta; depende en gran medida del estadio mental de la persona que se enfrenta a ofrecer una solución, para un niño pequeño puede ser un problema encontrar cuánto es 3 + 2. O bien, para niños de los primeros grados de primaria responder a la pregunta ¿Cómo repartes 96 lápices entre 16 niños de modo que a cada uno le toque la misma cantidad? le plantea un problema, mientras que esta pregunta sólo sugiere un ejercicio rutinario. Al percibir la realidad de lo difícil que era la resolución de problemas George pólya contribuye con cuatro fases o pasos, los cuales se describen a continuación: -Entender el problema Este primer paso trata de imaginarse el lugar, las personas, los datos, el problema. Para eso, hay que leer bien, replantear el problema con sus propias palabras, reconocer la información que proporciona, hacer gráficos, tablas. A veces se tiene que leer más de una vez.  Diseñar un plan En esta etapa se plantean las estrategias posibles para resolver el problema y seleccionar la más adecuada.  Ejecutar el plan Ya se tiene el plan seleccionado, así que se aplica. Se Resuelve el problema, monitorear todo el proceso de solución.  Examinar la solución Luego de resolver el problema, revisar el proceso seguido. Cerciorarse si la solución es correcta, si es lógica y si es necesario, analizar otros caminos de solución. 10 Borragán (2006) comenta que según Pólya, en la solución de un problema los estudiantes aplican las cuatro operaciones mentales de manera flexible; esto quiere decir; que éstos pasos no se trabajan necesariamente en una secuencia lineal. Gráfica 1 Operaciones mentales plantadas por Pólya Chavez, G (2003) Método pólya. El pensamiento del Estratega. México; Plaza y Valdés, S.A. de C.V. A pesar de que los estudios de George Pólya no son teóricos ni sistemáticos sino más bien a través de observaciones, uso de estrategias y reglas lógicas plausibles y generalizadas que guían la solución de problemas.

BIBLIOGRAFÍA: http://recursosbiblio.url.edu.gt/tesisjcem/2015/05/86/Escalante-Silvia.pdf

DEFINICIÓN DE ALGORITMO DE SOLUCIÓN.

Técnicas de diseño de algoritmos -Estrategia Greedy Un algoritmo Greedy elige, en cada paso, una solución local optima. Las estrategias greedy encuentra una solución máxima al problema. (ejem. Rutas de entrega) -Programación dinámica Es un método para reducir el tiempo de ejecución de un algoritmo mediante la utilización de sub problemas superpuestos y sub estructuras óptimas. Una sub estructura óptima significa que soluciones óptimas de sub problemas pueden ser usadas para encontrar las soluciones óptimas del problema en su conjunto. Se pueden resolver problemas con sub estructuras óptimas siguiendo estos tres pasos: Dividir el problema en sub problemas más pequeños. Resolver estos problemas de manera óptima usando este proceso de tres pasos respectivamente. Usar estas soluciones óptimas para construir una solución óptima al problema original. -Inducción A través de la inducción matemática se puede definir un mecanismo para encontrar todos los posibles elementos de un conjunto semicursivo partiendo de un subconjunto conocido, o bien, para probar la validez de la definición de una función re cursiva a partir de un caso base. 

BIBLIOGRAFÍA: https://www.monografias.com/trabajos107/diseno-algoritmos-solucion-problemas/diseno-algoritmos-solucion-problemas2.shtml

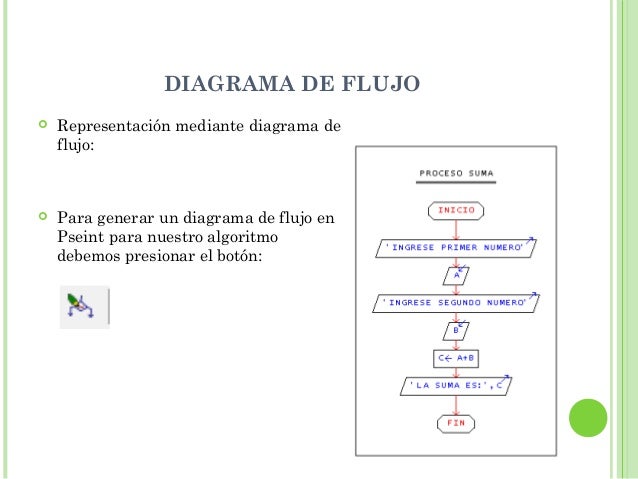
¿QUÉ ES UN DIAGRAMA DE FLUJO?

Un diagrama de flujo es un diagrama que describe un proceso, sistema o algoritmo informático. Se usan ampliamente en numerosos campos para documentar, estudiar, planificar, mejorar y comunicar procesos que suelen ser complejos en diagramas claros y fáciles de comprender. Los diagramas de flujo emplean rectángulos, óvalos, diamantes y otras numerosas figuras para definir el tipo de paso, junto con flechas conectoras que establecen el flujo y la secuencia. Pueden variar desde diagramas simples y dibujados a mano hasta diagramas exhaustivos creados por computadora que describen múltiples pasos y rutas. Si tomamos en cuenta todas las diversas figuras de los diagramas de flujo, son uno de los diagramas más comunes del mundo, usados por personas con y sin conocimiento técnico en una variedad de campos. Los diagramas de flujo a veces se denominan con nombres más especializados, como "diagrama de flujo de procesos", "mapa de procesos", "diagrama de flujo funcional", "mapa de procesos de negocios", "notación y modelado de procesos de negocio (BPMN)" o "diagrama de flujo de procesos (PFD)". Están relacionados con otros diagramas populares, como los diagramas de flujo de datos (DFD) y los diagramas de actividad de lenguaje unificado de modelado (UML).

BIBLIOGRAFÍA: https://www.lucidchart.com/pages/es/qu%C3%A9-es-un-diagrama-de-flujo